Equation for Data Stream Density
In the article Data Stream Energy Density, the Author provided an equation for Data Stream Density that was presumably derived in the Data Stream Momentum Notebook of 1994. This was the equation that the Author provided.
Current Equation
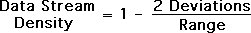
Data Stream Density is equivalent to the inertial component of a data stream, its resistance to change.
Range refers to the possible range of the data stream.
Deviation is the range of variation of the data stream. The Living Algorithm produces this central measure.
However, the above equation is not the same as the one in the Data Stream Momentum Notebook. This article is devoted to explaining why.
Data Stream Density 1994
This is the original equation the Author derived in 1994.
Original Equation
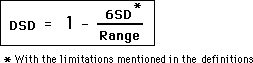
As DSD are the initials for Data Stream Density, the only difference in the 2 equations is the numerator of the expression on the right. In the initial equation the value of the numerator is '2 Deviations'. In the above equation that same value is '6SD' – 6 Standard Deviations. Further this expression is accompanied by an asterisk * that is linked to the words, 'With the limitations mentioned in the definitions'.
This significant difference has a simple reason. When the Author derived the original equation for data stream density, he had not yet derived an equation for the Deviation of a Data Stream. In fact, he hadn't even explored the advantages of the Living Average, nor was he aware of anything like Data Stream Derivatives. In some ways, he was at the raw beginning of his lifelong obsession and he was building his foundation.
Accordingly, the original proof is based around the mean averages and standard deviations of Probability, not the decaying averages and deviations of the Living Algorithm System. The averages drop out as an expression in the derivation, so are not an issue. The Data Stream's Range, one of the remaining factors, is the same no matter which system is employed. In the Current Equation, the Author employs the Deviation from the Living Algorithm System to characterize the data stream's range of variation. In the Original Equation he employed the Standard Deviation to characterize this same range of variation, as he didn't even know what a Deviation was. In the Current Equation for DSD there are 2 Deviations, while in the Original Equation there are 6SD. Why the difference in the coefficients?
How did the Author determine the coefficients of the Standard Deviation in the Original Equation? Let's quote the original article, written so long ago:
"The three standard deviations is an arbitrary choice. We could just as well have chosen 4 SD, 2 SD, or maybe even 2 Average Deviations, depending upon the constraints of the experiment. We are merely defining the probable area that the Data might fall within."
In other words the coefficient, an arbitrary choice at the time, was only meant to determine probable area, as per his discussion of data streams. (Note: The reference to Average Deviations was added much later, after he derived his equation for what he then called the Average Deviation.) Now 20 years later, we don't need to make an arbitrary choice regarding the coefficient of the Deviation. Let's see why.
The original derivation still holds true, no matter which system we choose. The Living Algorithm specializes in digesting data streams, while Probability specializes in processing data sets. Because we are characterizing the density of a data stream, we will employ the Living Algorithm's Deviation in our derivation rather than Probability's Standard Deviation.
Let's start with the Current Equation, but replace the unknown coefficient with a question mark '?'.
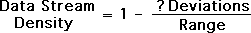
We know the Density of a Random Data Stream is 0. This is true by definition, as a Random Data Stream has no substance. As such this fact is a given.

We also know that the Deviation of a Random Data Stream is equal to half the range. In other words, it is equally probable that the next value in a random data stream can be anywhere within the range.

Let's plug these values in our Data Stream Density equation with the unknown coefficient '?".
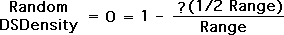
The Range drops out of the equation, as the Range divided by itself equals 1. We then perform standard algebraic manipulations to determine that the coefficient '?' equals 2.
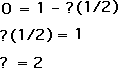
This gives us our Current Equation for Data Stream Density with the coefficient equal to 2.
![]()
This establishes the logic behind this crucial equation for Data Stream Density, the inertial component of a data stream.